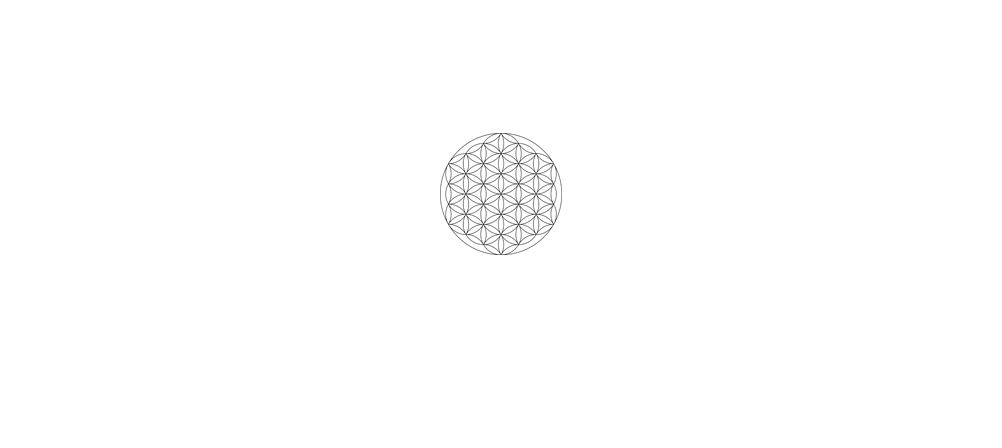

In nature, we find patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances.
They are also symbolic of the underlying metaphysical principle of the inseparable relationship of the part to the whole. It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity. This principle of interconnectedness, inseparability and union provides us with a continuous reminder of our relationship to the whole, a blueprint for the mind to the sacred foundation of all things created.
Starting with what may be the simplest and most perfect of forms, the sphere is an ultimate expression of unity, completeness, and integrity. There is no point of view given greater or lesser importance, and all points on the surface are equally accessible and regarded by the center from which all originate. Atoms, cells, seeds, planets, and globular star systems all echo the spherical paradigm of total inclusion.

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each corner or vertex. It has six edges and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has four faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.
For any tetrahedron the vertices lie on a sphere called the circumsphere, while another sphere the insphere just touches the tetrahedron's faces.
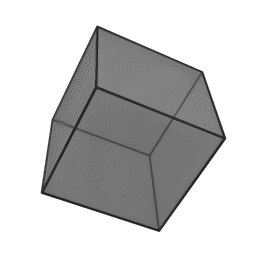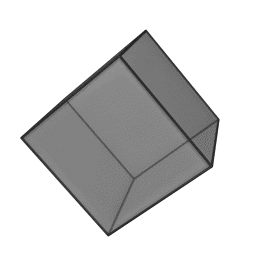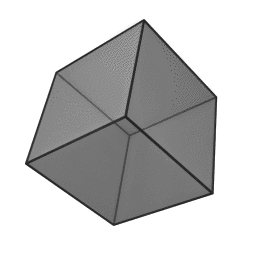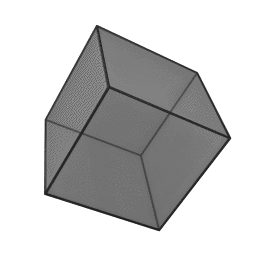
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each corner or vertex. It has six edges and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has four faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.
For any tetrahedron the vertices lie on a sphere called the circumsphere, while another sphere the insphere just touches the tetrahedron's faces.
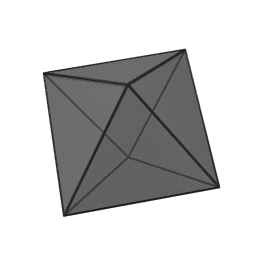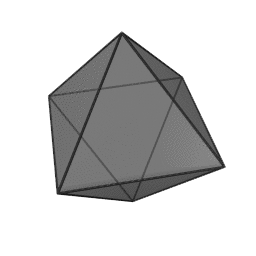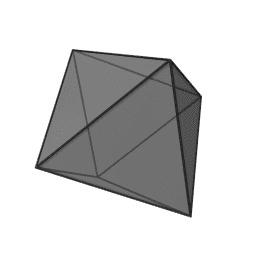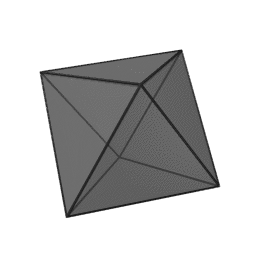
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each corner or vertex. It has six edges and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has four faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.
For any tetrahedron the vertices lie on a sphere called the circumsphere, while another sphere the insphere just touches the tetrahedron's faces.
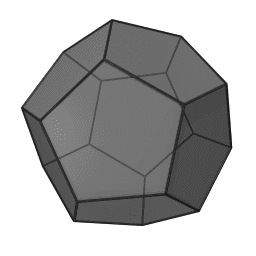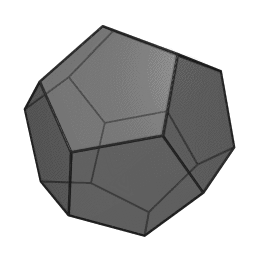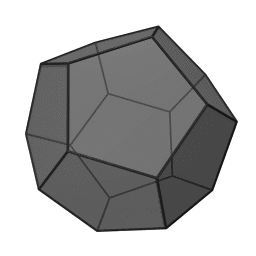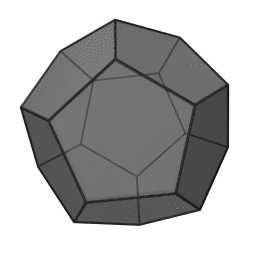
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each corner or vertex. It has six edges and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has four faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.
For any tetrahedron the vertices lie on a sphere called the circumsphere, while another sphere the insphere just touches the tetrahedron's faces.

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each corner or vertex. It has six edges and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has four faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.
For any tetrahedron the vertices lie on a sphere called the circumsphere, while another sphere the insphere just touches the tetrahedron's faces.